개발 공부 - [검색트리] 레드블랙트리 - 3

DELETE

- 보통의 BST 에서처럼 DELETE 한다.

- 실제로 삭제된 노드 y가 red면 종료.

- y가 black이었을 경우 RB-DELETE-FIXUP 을 호출한다.

* 수도 코드내 삭제되는 x는 y가 자식이 있었을 경우 그 자식노드로 대치, 

없었을 경우 NIL 노드로 대치

RB-DELETE-FIXUP(T,x)

x가 NIL 노드일 수도 있다. 그리고 x가 red일 경우 쉽게 해결할 수 있다. 이 두가지를 기억한다. 실제로 DELETE에서 문제는 x가 BLACK인 경우다.

각 노드는 red 혹은 black이다.

: 문제 없음. 루트노드는 black이다.

y가 루트였고, x가 red인 경우 위반된다. 하지만, 심각한 문제는 아니다.

모든 리프노드(즉, NIL 노드)는 black이다.

: 문제 없음

red노드의 자식노드들은 전부 black이다.(즉, red노드는 연속되어 등장하지 않고)

p[y]와 x가 모두 red일 경우 위반

x가 레드인 경우 red를 black으로 바꾸어 주면 되기 때문에 심각한 문제는 아니다.

모든 노드에 대해서 그 노드로 부터 자손인 리프노드에 이르는 모든 경로에는 동일한 개수의 black노드가 존재한다.

원래 y를 포함했던 모든 경로는 이제 black노드가 하나 부족하다.

노드 x에 "extra black"을 부여해서 일단 조건5를 만족시킨다. 색을 두개 가지고 있게 하는 임시 방법이다.

그렇게 되면 노드 x는 "double black" 혹은 "red & black"이 된다. 앞으로 해결해야하는 문제가 이 것을 블랙노드로 바꾸는 것이다.

수정 아이디어

- extra black 을 트리위쪽으로 올려보낸다.

- x가 red&black 상태가 되면 black 처리하고 끝냄

- x가 루트가 되면 그냥 extra black을 제거

Loop Invariant

- x는 루트가 아닌 double-black 노드

- w는 x의 형제노드

- w는 NIL 노드가 될 수 없음

----------------------------------------------참조----------------------------------------------

DELETE의 경우 8가지 case로 분류할 수 있다. INSERT와 마찬가지로 1,2,3,4와 5,6,7,8은 대칭이다.

• Case 1,2,3,4 : x가 부모의 왼쪽 자식노드인 경우

  • x는 double black노드이거나, NIL 노드 일수도 있다.

  • x의 형제노드인 w노드는 반드시 존재하고, NIL일 수는 없다.

  • x는 자신의 부모의 왼쪽 자식이다.

• Case 5,6,7,8 : x가 부모의 오른쪽 자식노드인 경우

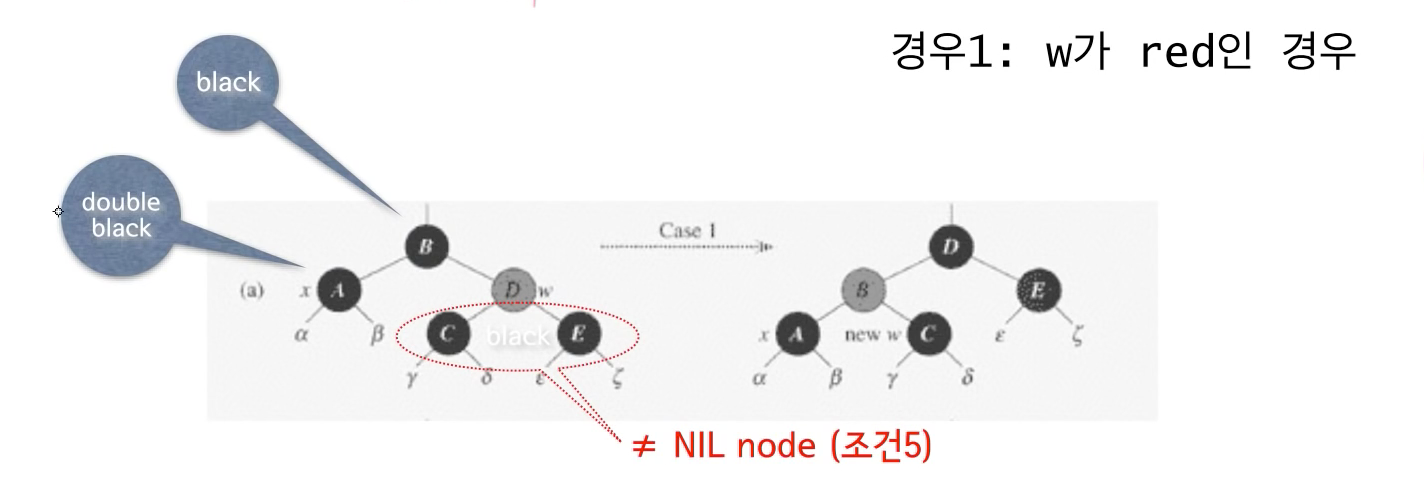
Case 1 - x의 형제노드 w가 RED인 경우

• Case 1,2,3,4의 공통 조건에 해당하며, 케이스 1인 경우는

• x의 형제노드 w가 RED인 경우이다. 이 경우는 자식노드가 NIL일 수 없고, BLACK 노드이다.

• 이 상황에서 문제를 해결하기 위해,

• w를 BLACK으로 p[x]를 RED로 바꾼 뒤

• p[x]에 대해서 left-rotation을 적용한다. x는 여전히 double-black 노드를 가지고 있다.

• x의 새로운 형제노드는 원래 w의 자식노드이다.

• 따라서, 새로운 w노드는 black노드이다. 이 경우 Case 2, 3, 4로 넘어가게 된다.

• 정리를 하면, Case1의 경우 x의 부모 노드에 대해서 left-rotation을 적용하면, 새로운 w노드가 red가 아닌 black이 되는 상황이라서 Case 2, 3, 4로 넘어가게 된다.

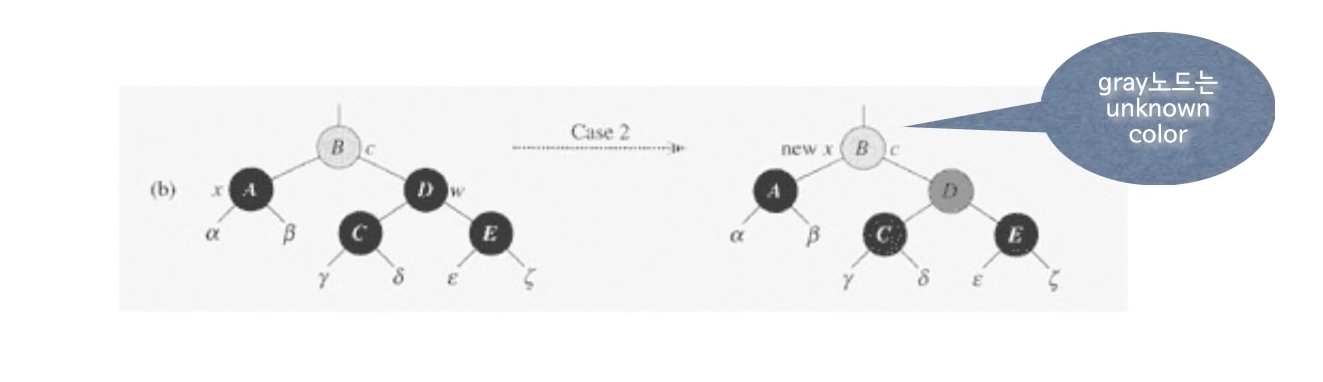
Case 2 - w는 BLACK, w의 자식들도 BLACK인 경우

• case 2, 3, 4의 경우 x의 형제노드 w가 BLACK인 경우이다. 이 중에서 w의 자식들도 모두 BLACK인 경우가 Case 2에 해당한다.

• 이 경우, x와 w가 모두 블랙이므로 부모인 B노드는 RED 일수도 있고, BLACK 일수도 있다.

• 현재 x는 double black 노드이고, w는 black 노드이다.

• 이 상황에서 x와 w로부터 black을 하나씩 뺏어서, 부모노드에게 준다.

• 결과적으로 x는 extra black이 하나 없어졌으므로 BLACK노드가 됐고, w는 black을 뺏겼으므로 RED노드가 된다.

• 다음으로 p[x]에게 extra-black 노드를 준다. 이렇게 하면, 트리의 위에서 부터 내려오면서 유지하던 BLACK노드의 갯수가 유지 된다.

• 만약 p[x]가 RED였다면, 위에서 설명했던 것처럼 red & black을 가지고 있는 노드를 BLACK노드로 만들고 끝내면 되고, p[x]가 BLACK이었다면 p[x]를 새로운 x로 해서 계속한다.

• 만약 Case1에서 Case2에 도달한 경우면 p[x]는 red였고, 따라서 새로운 x는 red & black이 되어서 종료된다.

• 하지만 Case2로 바로 온 경우에 p[x]가 원래 BLACK이었다면, p[x]가 double black이 되므로 반복해서 문제를 해결해야 할 수도 있다.(뒤에서 설명) 다만, extra-black이 한 level 올라갔다.

Case 3 - w는 BLACK, w의 왼쪽자식이 RED

• w를 RED로, w의 왼쪽자식노드를 BLACK으로 바꾼다.

• w에 대해서 right-rotation을 적용한다.

• x의 새로운 형제 w는 오른자식이 RED이다. 이것은 경우 4에 해당한다.

Case 4 - w는 BLACK, w의 오른쪽자식이 RED

• w의 색을 현재 p[x]의 색으로(unknown color)

• p[x]를 BLACK으로, w의 오른자식을 BLACK으로 바꾼다.

• p[x]에 대해서 left-rotation을 적용한다.

• x의 extra-black을 제거하고 종료한다.

• 이렇게 되면, double-black노드가 없어졌음에도 불구하고, 기존의 A노드를 지나는 블랙노드의 갯수가 로테이션 전과 똑같아 진다. 그리고 나머지 C와 E를 지나는 블랙노드의 갯수도 기존과 동일하게 유지된다.

출처: https://ict-nroo.tistory.com/73?category=698685 [개발자의 기록습관]

시간 복잡도

- BST에서 delete : O(log2n)

- RB-Delete-Fixup : O(log2n)